La Teoria del Desdoblamiento del Espacio y del Tiempo
¿POR QUÉ UN DESDOBLAMIENTO?
Caracterizado por un movimiento, una curiosa velocidad y una ecuación universal, el desdoblamiento del espacio y del tiempo explica a la vez lo infinitamente pequeño de nuestras partículas, lo infinitamente grande del universo… y nosotros, perdidos en una tierra inmensa, planeta de un pequeñísimo sistema solar cuyas dimensiones nos parecen infinitas.
Tan solo tenemos que admitir que puedan existir tiempos imperceptibles atrapados entre dos tiempos perceptibles.
El tiempo entre una pregunta (un obstáculo cualquiera) y su respuesta (franqueo del obstáculo) define un tiempo de adaptación para una partícula, que utiliza ese tiempo en su espacio definido y limitado por su horizonte. Una aceleración del transcurso del tiempo en un horizonte imperceptible, desdoblado del primer horizonte, permite a una partícula, desdoblada de la partícula inicial, evolucionando de la misma manera, obtener la respuesta antes que la partícula inicial.
La aceleración del tiempo puede ser tal que la partícula inicial “no tiene tiempo” de utilizar un “instante” de su tiempo mientras que la partícula desdoblada “tiene todo el tiempo” de obtener la respuesta a su pregunta “en ese mismo instante”. Eso necesita de poder acelerar el tiempo al tiempo que desdoblando la partícula inicial en tiempos imperceptibles que yo he llamado “aperturas temporales”.
Ahora bien, el tiempo es observable y medible por el movimiento de un espacio en relación a otro. Debido a ello es continuo. Diferenciar el tiempo en “aperturas temporales” viene a ser, diferenciar la observación de un movimiento, o sea que la percepción del observador mismo, que es a la vez horizonte de partículas y partícula en su horizonte.
El desdoblamiento implica un observador desdoblado evolucionando en aperturas temporales del observador inicial. Debido a una diferencia de percepción, el observador desdoblado evoluciona rápidamente en un tiempo acelerado que él considera como normal.
Así pues, él ignora al observador inicial ya que desconoce su tiempo de evolución que le aparece a él como fijado.
Él puede considerarse como un observador inicial que a su vez se desdobla. Un 3er observador responde pues a las preguntas del 2º realizándose él también otras preguntas.
Por intercambios de información en “aperturas temporales” imperceptibles, el 1er observador puede obtener respuestas a preguntas que no ha tenido tiempo de hacerse. Esto le permite conocer las respuestas del 3º antes que del 2º al cual puede pues guiar sugiriéndole nuevas preguntas que modifican su memoria instantáneamente.
Es decir, el 2º observador evoluciona en su presente. Responde a las preguntas del 1º que le parecen proceder del pasado. Se realiza preguntas las cuales son respondidas a su vez por el 3º. Esas respuestas parecen estar en su futuro. Por los intercambios de información instantáneos en las aperturas temporales, es pues, al mismo tiempo, observador en los tres tiempos diferentes: pasado, presente, futuro.
La teoría del desdoblamiento da una ecuación que permite expresar de manera rigurosa el cambio de percepción entre dos observadores desdoblados en dos tiempos diferentes.
Esta ecuación es la base fundamental de la teoría del desdoblamiento. Por un cambio de escala de espacio y de tiempo, reúne lo infinitamente grande de un observador inicial y lo infinitamente pequeño del observador desdoblado.
EL MOVIMIENTO DE DESDOBLAMIENTO
Todo parte de un circulo Ω que gira sobre sí-mismo. Su radio gira con una velocidad de rotación constante φ:
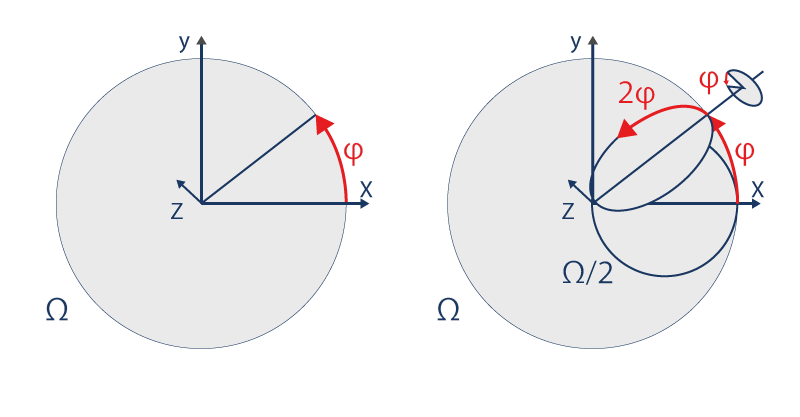
Ahora bien, este radio es el diámetro de un circulo Ω/2 dos veces más pequeño que gira sobre si-mismo dos veces más rápido, al tiempo que gira en el espacio, alrededor de su diámetro con la misma velocidad φ. Este círculo Ω se encuentra como en un tiovivo. Tomando el lugar, el circulo Ω/2 sigue el movimiento, pero girando sobre si-mismo, al tiempo que realizando una pirueta.
Este movimiento fundamental sigue adelante con el circulo Ω/4 = 2α dos veces más pequeño que el circulo Ω/2, él mismo dos veces más pequeño que el circulo Ω…
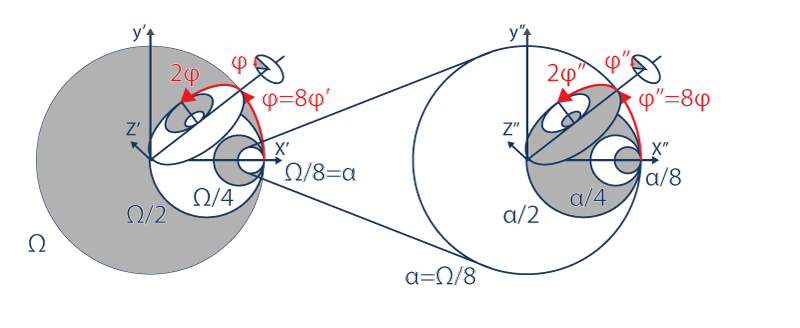
Y así sucesivamente en lo infinitamente pequeño:
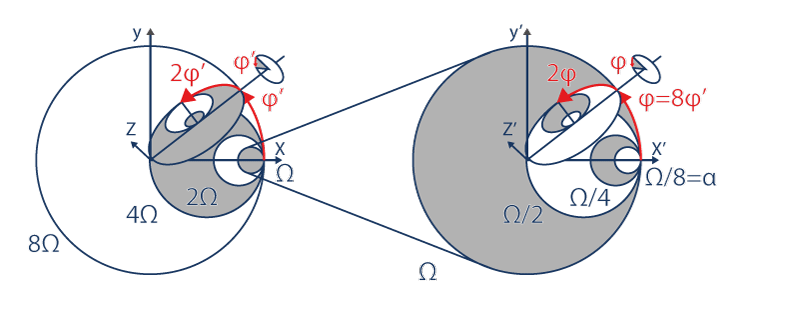
Como en lo infinitamente grande:
Una visualización del movimiento por ordenador nos muestra los trayectos de las partículas sobre los diferentes círculos encajados en el mismo movimiento:
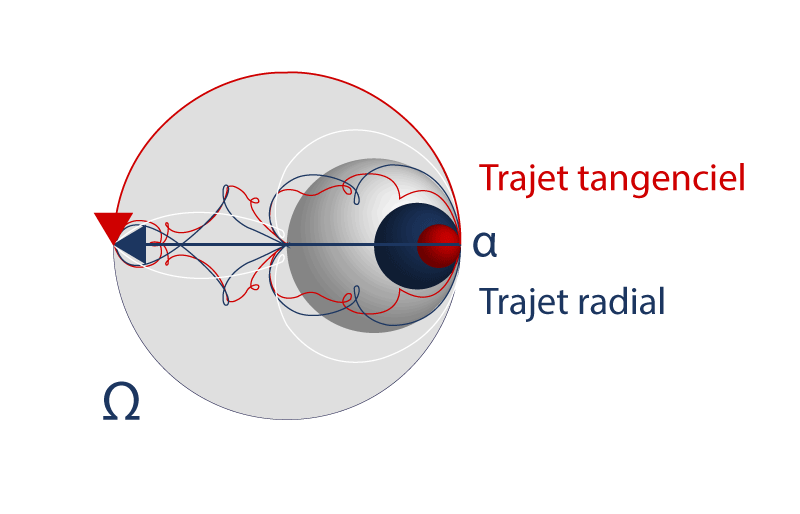
Salvo el trayecto tangencial que da la vuelta, todos los demás trayectos pasan por el centro. De ahí la lógica de las apelaciones: trayecto radial y trayecto tangencial.
La ecuación del movimiento es:
X = cos²φ(cosφ – sin²φ) Y = cos²φsinφ(1 + cosφ) Z = – cosφsin²φ
Ciertamente las curvas radiales son algo más complicadas, pero en realidad solo son importantes el principio y el final del desdoblamiento de la partícula α en su horizonte Ω. Podemos pues representar de manera muy esquemática este movimiento de desdoblamiento sobre el eje del horizonte Ω:
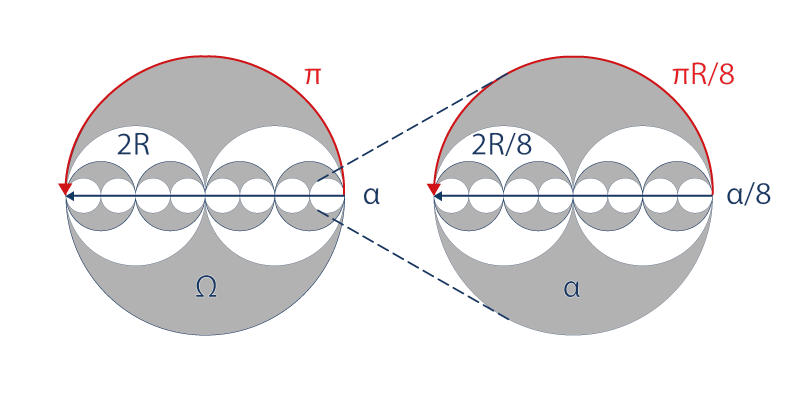
Podremos decir que este movimiento de desdoblamiento es universal en lo infinitamente pequeño como en lo infinitamente grande si la partícula α es el horizonte de su partícula α/8 y si su horizonte Ω es la partícula de su propio horizonte 8Ω.
Esta ley del desdoblamiento podría pues ser llamada “la ley del alfa y del omega”, una ley que dirige las estrellas, los planetas, el sorprendente Big-bang – tan mal entendido como la inflación inicial – la aceleración aparente actual de la expansión del universo… y su próxima contracción!
Una ley que, obviamente, necesita una inteligencia suprema capaz de ponerla en aplicación y que sería a la vez ¡el alfa y el omega, el principio y el final!
En lo infinitamente pequeño la energía no llega de manera continua. Es distribuida de manera discontinua por “quanta” de energía: cada “quantum” estando separado del siguiente por un tiempo imperceptible, casi nulo, pero en donde las partículas disponen sin embargo de una energía infinita. Es el famoso “Principio de Heisenberg”: para simplificar digamos que, para una partícula, la energía disponible, multiplicada por el tiempo perceptible pero casi nulo de esta disponibilidad es superior o igual a la constante de Planck. Por consiguiente, si ese tiempo parece nulo para un observador, esta energía le parece infinita. En realidad, el tiempo nulo no existe… Esta sucesión de quanta de energía da la sensación de una continuidad para los observadores que somos. ¡Nada de eso! De ahí la apelación de mecánica “cuántica” para lo infinitamente pequeño de las partículas.
El desdoblamiento se justifica fácilmente por la idea siguiente: una partícula se desdobla para introducirse en el interior de un universo y adquirir allí nuevos conocimientos, al tiempo que lo rodea, guardando de esta manera intacta su memoria. ¡Pero eso no se para ahí! Hemos visto que la partícula desdoblada hace lo mismo con un universo dos veces más pequeño y demás y demás…
Es de esta manera que un trayecto tangencial es también un trayecto radial que pasa por el centro de un universo dos veces más grande. De la misma manera, un trayecto radial es un trayecto tangencial de un universo dos veces más pequeño.
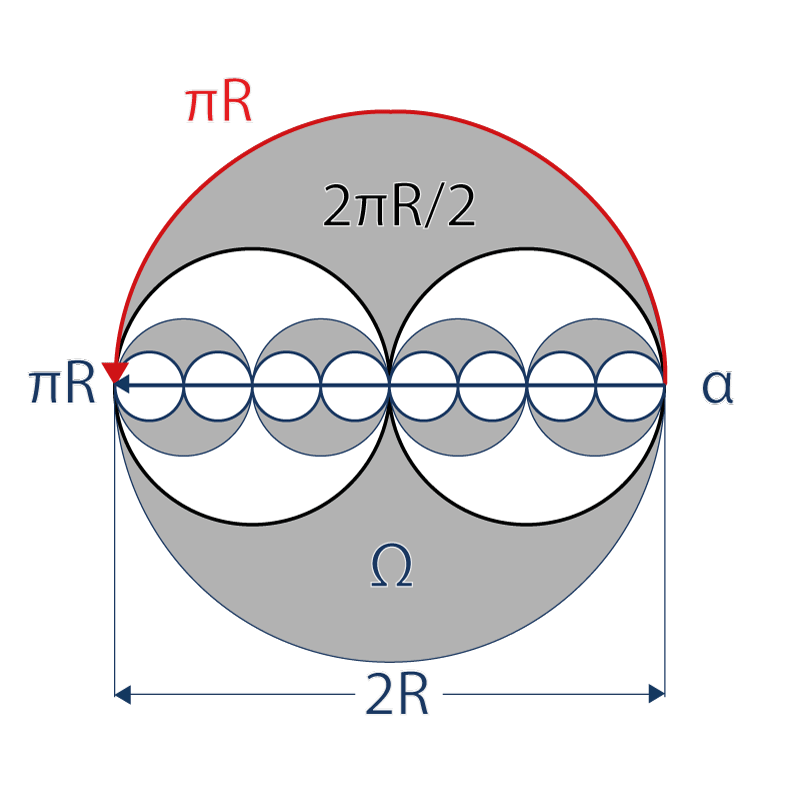
Siempre podemos decir que, desdoblada de una partícula tangencial, una “partícula radial” es una “partícula tangencial” que se desdobla para explorar sin peligro un universo dos veces más pequeño.
Sin embargo, será interesante saber por qué, cuándo y cómo este desdoblamiento está limitado en el tiempo y en el espacio.
En el horizonte inicial hemos visto que el trayecto radial de un trayecto tangencial es pues siempre igual a πR, si 2R es el diámetro del trayecto tangencial inicial y π = 3,14… Llamado irracional, este número sin fin existe en un punto, pequeña cosa circular de radio casi nulo. Existe también con una recta que es un circulo de radio infinitamente grande o un horizonte tangencial lejano.
Podemos decir más sencillamente que un trayecto radial es el diámetro de un horizonte. Está constituido por una sucesión de n pequeños círculos de nada. El diámetro de Ω es igual a 2R para un observador externo que considera este círculo como el horizonte de una pequeña partícula; debe de ser igual a πR para un observador interno que considera este mismo circulo como el horizonte lejano de su inmenso universo.
En efecto, a través de un horizonte Ω, un trayecto radial está constituido esquemáticamente por una sucesión de n pequeños círculos α (trayectos radiales), de radio R/n, en donde n es un número entero. Sea cual sea n, es igual a nπR/n = πR :
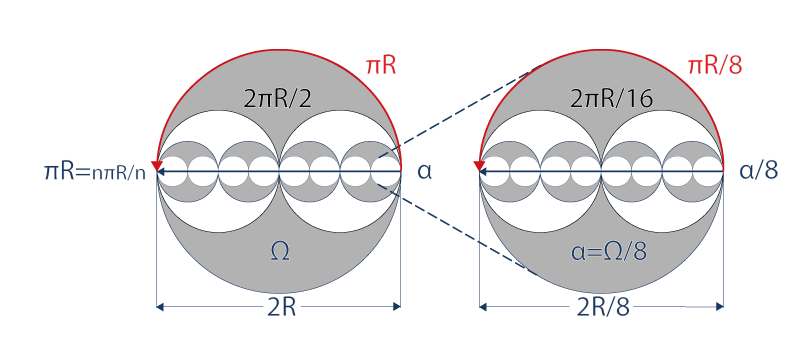
LA ECUACIÓN DEL DESDOBLAMIENTO
Acelerar el movimiento de desdoblamiento y dilatar un espacio para hacerlo imperceptible en el espacio inicial solo es interesante si el observador del espacio inicial se desdobla igualmente en el espacio imperceptible. De esta manera, aun siendo el observador del espacio inicial, su “doble” puede observar el espacio desdoblado en un tiempo que no tiene tiempo de existir en el espacio inicial.
Es pues indispensable conocer la relación que permite cambiar de observación entre dos tiempos desdoblados, evolucionando en dos tiempos diferentes pero en el mismo plano de observación.
La teoría del desdoblamiento se basa en una ecuación universal que permite pasar del observador interno (que recorre un trayecto radial igual a πR en un espacio dilatado y acelerado) al observador externo (para quien ese mismo trayecto radial es el diámetro de ese mismo espacio: un diámetro igual a 2R):
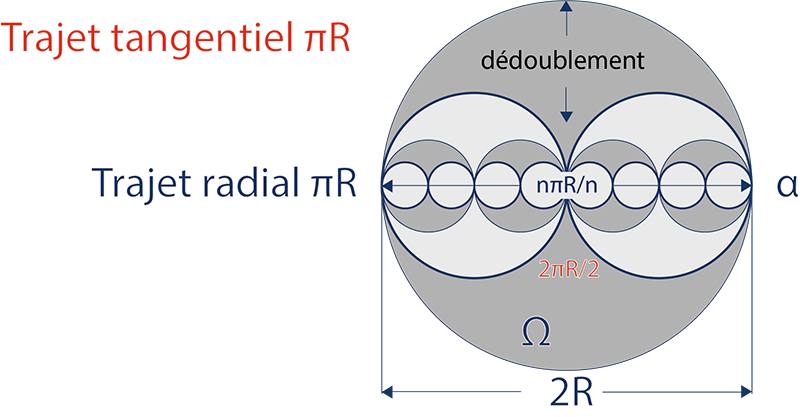
El observador interno ignora el diámetro 2R de su horizonte dilatado Ω’ que se ha vuelto igual al horizonte inicial Ω en el plano inicial, pero en un tiempo imperceptible del observador inicial.
Para el observador interno, este diámetro D es el trayecto radial πR de una partícula que gira sobre si-misma:
D = πR.
Correspondiente a ese diámetro D, el horizonte aparente le aparece pues como siendo la media circunferencia, que, como toda media circunferencia, es igual a ½ πD.
O sea que, para este observador interno, tenemos la relación:
½ πD = ½ π(πR) = π²R/2.
Sin embargo, la rotación π percibida por el observador interno corresponde, para el observador externo, al diámetro aparente 2R del horizonte Ω.
Así que (π²)⁻ para el observador interno, escrito (-),
Se vuelve (4R²)⁺ para el observador externo, escrito (+).
No obstante, el radio R, percibido por el observador externo es, para el observador interno, igual al trayecto radial π/8 debido a la dilatación de la partícula que se vuelve 8 veces más gorda en una 9ª rotación π/8.
Así que (R/2)⁺ para el observador externo (+),
Se vuelve (π/16)⁻ para el observador interno (-).
O sea que: [(π²)(R/2)]⁺ se convierte en [(4R²)(π/16)]⁻ = (πR²/4)⁻.
Ahora bien, el observador externo (+) percibe la ½ circunferencia πR, deducimos que (πR²/4)⁻ del observador interno (-) es igual a (πR)⁺ del observador externe (+).
De ahí la ecuación fundamental del cambio de percepción del tiempo y del espacio entre el observador interno (-) y el observador externo (+):
(πR²)⁻ = (4πR)⁺
Considerando la variable R y derivando el primer miembro de la ecuación πR², obtenemos solo la mitad del segundo miembro: (4πR)/2.
¿Dónde está la otra mitad? No hay que olvidar que el movimiento de rotación se acelera, π se vuelve 2π en un tiempo imperceptible y en un espacio 2 veces más grande en donde el resultado se vuelve exacto y observable en el tiempo del observador.
El lenguaje matemático permite decirlo de otra manera:
Considerando la variable R y derivando el primer miembro de la ecuación πR², obtenemos la mitad del segundo miembro 2πR. A la inversa, integrando 2πR, reencontramos πR². Pero ¡ese radio R es una constante! Ahora bien, la derivación de una constante da cero y la integración de cero – operación aparentemente inversa – no existe… a menos que ¡cero no exista!
En este desdoblamiento del tiempo, la integración siempre tiene que ver con un número infinitamente pequeño. Haría pues falta que la derivación de una constante dé otra constante infinitamente pequeña e imperceptible en nuestro tiempo, lo cual evidentemente no está admitido en las matemáticas actuales en donde cero sigue siendo un cero absoluto. Pero el hecho sigue siendo que, en el universo, debido al desdoblamiento del tiempo, el cero absoluto no puede existir, si no la observación ya no sería posible y debido a ello, el observador se volvería totalmente inútil.
Todos los matemáticos de la antigüedad sabían que el cero no existía. ¿No sería eso consecuencia del conocimiento del movimiento de desdoblamiento?
LA VELOCIDAD DE LA LUZ
Por una comprobación del movimiento de desdoblamiento en nuestro sistema solar y una justificación rigurosa de los movimientos planetarios, conforme con el movimiento fundamental de desdoblamiento definido en la teoría, la velocidad de la luz ha podido ser justificada y sobre todo calculada por 1ª vez (publicaciones 1998).
C₀ = trayecto radial / trayecto tangencial = 2(108πDs)10⁴ / 1 an = 299 792 km/s
Con el diámetro del Sol: Ds = 1 394 180 km.
La velocidad de la luz es la constante universal del movimiento de desdoblamiento. Por ello, el diámetro aparente de nuestro Sol debe absolutamente corresponder con este valor para los observadores que somos en nuestro sistema solar: esto es lo que ocurre hoy en día: como veremos más adelante, una modificación de este diámetro conlleva obligatoriamente una modificación del trayecto radial de la Tierra (1/2 año) que nos da la medida de nuestro tiempo. Esta modificación puede tener consecuencias caóticas para la Tierra y en todo el sistema solar.
Entendemos por fin la importancia fundamental de esta teoría del desdoblamiento del tiempo que pone el diámetro de nuestro Sol en primera fila de nuestra observación terrestre.
Lo mismo ocurre con las velocidades supralumínicas, necesarias al desdoblamiento del tiempo. En efecto, el movimiento de desdoblamiento las impone, y permite su cálculo (publicadas en 1998):
CC₂ = 7C₁ = (7³/12)10⁵C₀, dónde C₀ es la velocidad de la luz
Esta relación de velocidades limita el espacio y el tiempo del desdoblamiento.
Al final del ciclo aparece una 3ª velocidad supralumínica C₃ = 7C₂ que abre nuestro mundo a lo imperceptible. Veremos que este límite impone un número finito de 2ºs observadores desdoblados del 1º. Impone también un solo desdoblamiento del 2º que tendrá pues un solo doble para responder a sus preguntas.
Estableciendo la ecuación de la velocidad de la luz, me ha sido posible explicar de manera rigurosa el curioso postulado introducido por Einstein afirmando, sin justificación lógica, que la velocidad de la luz era independiente de la velocidad de la fuente y de la velocidad del observador. En efecto, C₀ es la velocidad de percepción del tiempo presente en un horizonte de observación en donde todos los diferentes observadores de ese mismo horizonte deben percibir todas las informaciones al mismo tiempo para ser parte de la misma realidad presente. Este sincronismo de observación es indispensable para que pueda existir un presente común a los diferentes observadores evolucionando en el mismo horizonte y el mismo tiempo.
Los postulados desaparecen
Para acelerar el tiempo, obligatoriamente se deben utilizar velocidades más grandes que C₀. Llamadas súper-luminosas, estas velocidades dan a otros observadores desdoblados la posibilidad de percibir la realidad más rápidamente. Desde hace algunos años científicos (A. Aspect 1982, N. Gisin 1998, A. Suarez 2002) han observado esas velocidades sin poder justificar su existencia. Esta justificación parecía imposible pues, según la ecuación de Einstein (E=mC²), una partícula debería tener una masa nula para alcanzar la velocidad de la luz. Como una información es una energía E, posee pues una masa m = E/C² que, debido a esta ecuación, no puede ir más rápido que la luz.
Podemos explicar esto de otra manera con la teoría del desdoblamiento:
- una masa nula en un horizonte, pasa a un horizonte imperceptible con una velocidad superlumínica en un tiempo imperceptible definido por el movimiento de desdoblamiento (que yo he llamado “apertura temporal”) en donde posee una masa.
- Una información que sobrepasa la velocidad de la luz cambia de tiempo. Es una ley puesta en evidencia por Langevin en 1923 (principio de los gemelos de Langevin) y comprobado experimentalmente en 1972 por Kneferle y Keating.
- Un cambio de escala muestra que un potencial al exterior de un horizonte expresado en 1/L (dónde L es una medida de espacio), se vuelve una fuerza en 1/L² para las partículas de ese horizonte.
- Una onda infinitamente grande en un horizonte se vuelve una onda infinitamente corta en otra en donde el tiempo está acelerado y dónde el observador ya no tiene la misma percepción del tiempo. Se ha podido mostrar que en el cero absoluto ((-273°K), un átomo perdía su lado corpuscular. Solo quedaba la información ondulatoria. Estaba previsto, pero no comprobado por Einstein, Podolsky, Rosen.
Las tres energías de desdoblamiento
Todas estas propiedades permiten hacer evolucionar en el mismo universo realidades (pasado, presente, futuro) que no se perciben y que son dependientes de tres velocidades y de tres energías de desdoblamiento de la cual la teoría del desdoblamiento da sus relaciones:
0,1%, 33,3% y 66,6% de la energía inicial
En 1998, Saul Perlmutter y Brian Schmidt mostraron, cada uno por su lado, por la observación de una supernova, que existía una energía de repulsión desconocida correspondiente al 66,7% de la energía del universo: recibieron el premio Nobel en el 2012. Esta observación ha confirmado el teorema de las tres energías de la teoría del desdoblamiento. En su día, Albert Einstein intentó introducir una constante cosmológica de 67%. No habiendo podido demostrarla, declaro dos años antes de su muerte, que esta constante había sido “el error más grande de su vida”, cuando, sin embargo, provenía de una intuición genial. Además de la observación de esos dos premios Nobeles, la teoría del desdoblamiento le da la razón.
Es acelerando el movimiento de desdoblamiento en un plano que se dilata que podemos cambiar de tiempo en un espacio a tres dimensiones observables.
